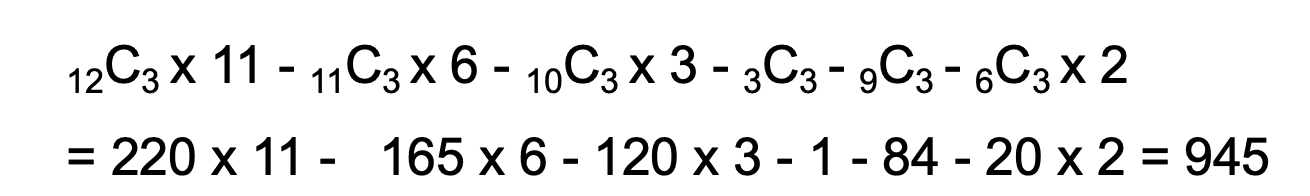11. 트리 위의 모임(13점)
위의 그림과 같은 트리 위의 세 사람이 세 정점 a, b, c 위에 한 명씩 서 있다. 이 세 사람이 한 정점에서 모이려면, 정점 v를 택해서, 각자 정점 v로 최단 거리로 이동해야 한다. 이 때 이동해야 하는 최단 거리의 합을 f(a, b, c) 라고 하자.
즉, d(i, j)가 정점 i와 정점 j 사이의 최단 거리라면, f(a, b, c) = minv{d(v, a) + d(v, b) + d(v, c)} 이다. 모든 1 ≤ a < b < c ≤ 12 쌍에 대해, f(a, b, c) 의 값을 모두 합치면 얼마인가?
========== 풀이 ==========
간선이 길이는 모두 1로 모두 같다.
모든 간선이 사용된 횟수를 구하면 쉽게 구할 수 있다.
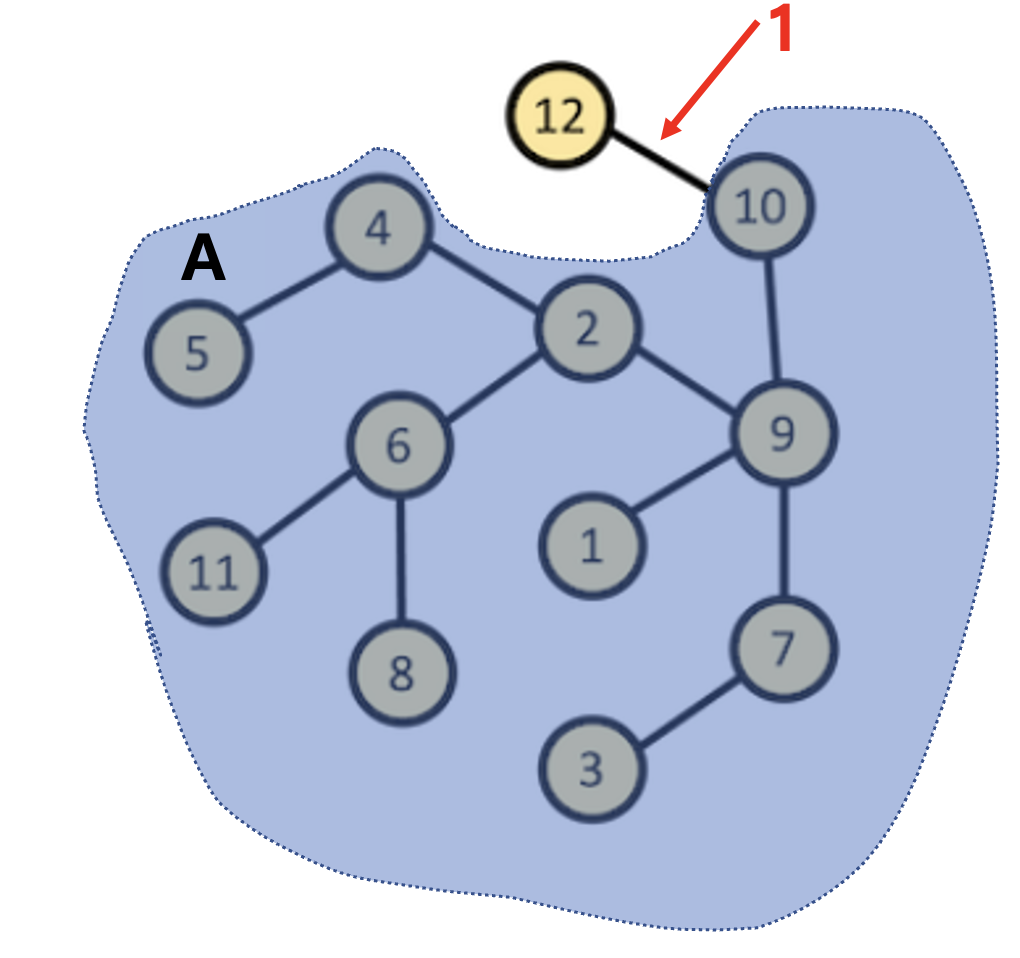1번 간선을 사용한 횟수는 12개의 정점에서 3개를 선택하는 경우에서 A영역에서만 3개가 선택된 경우를 빼면 된다.
12C3 - 11C3
이와 같이 12와 연결된 간선을 이용한 횟수는 정점 5, 11, 8, 1, 3과 연결된 정점이 사용 횟수와 같다.
(12C3 - 11C3) X
6
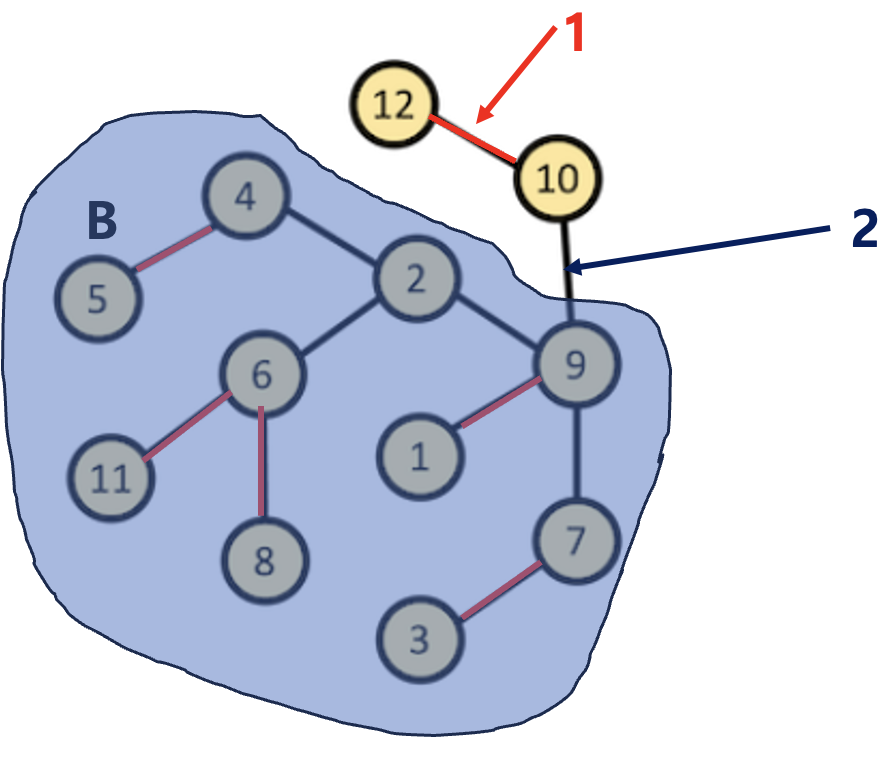
2번 간선을 사용한 횟수를 확인 하기 위해서는
전체 12개중 정점 3개를 선택하는 경우에서 B영역에서 3개가 선택되는 경우를 제외하면 된다.
12C3 – 10C3
이와 같은 경우가 (5,4), (3,7)이 더 존재 하므로
(12C3 – 10C3 ) X 3
가 된다.
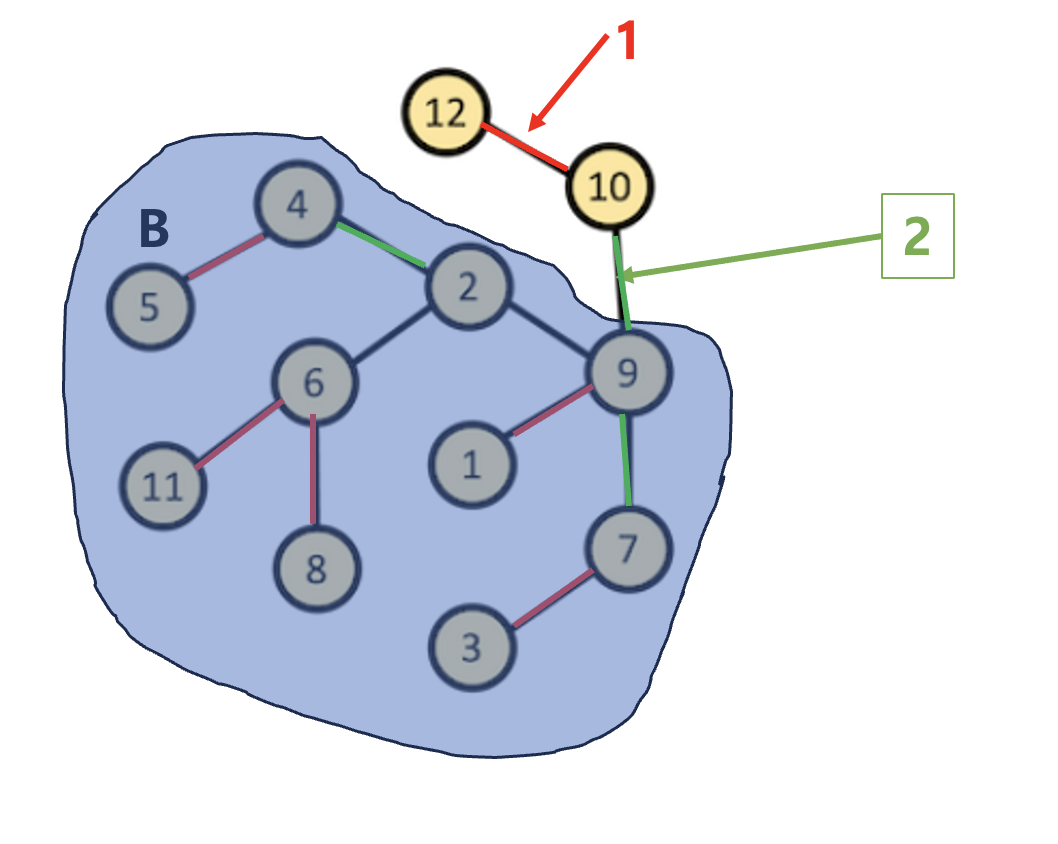이제 2개의 간선만 체크를 하면 된다.
그리고 2와 6사이의 간선은
전체 12개중 3개의 정점을 선택하는 경우에 다가
6,11,8에서 3개가 선택되는 경우와 나머지 9개에서 3개가 선택되는 경우를 제외하면 된다.
12C3 – 3C3 – 9C3
마지막으로 2와 9사이 간선은 12개 중 3개의 정점을 선택하는 경우에 다가
우측 6개중 3개를 선택하는 경우와 좌측 6개중 3개를 선택하는 경우를 제외하면 된다.
12C3 – 6C3 – 6C3
정답 945
